Почему большинство людей неправильно оценивают доходность хедж-фондов
Введение
Большинство критики доходности хедж-фондов связано с неправильным сравнением. Когда говорят, что хедж-фонды «уступают рынку», сравнивают лодку с автомобилем и жалуются, что лодка медленно едет по шоссе. Это верно, но смысл такого сравнения полностью теряется.
Покупка S&P, то есть рыночного фактора, стоит 9 базисных пунктов в год. Элитные хедж-фонды берут примерно 800–1600 б.п. в год (2/20 плюс дополнительные комиссии — это стандартная планка). Разница в стоимости — буквально в 100 раз.
Если бы оба продукта давали одинаковый результат, аллокаторы поступали бы неразумно. Но продукты разные, и крупные институциональные инвесторы, вкладывающие сотни миллиардов долларов в эти фонды, понимают это.
Они покупают то, что невозможно повторить ни за какие деньги: факторно-нейтральную доходность с высоким коэффициентом Sharpe и отсутствием корреляции на большом объеме. Когда вы понимаете, что это значит, премия за стоимость становится оправданной, и сравнение хедж-фонда с индексным фондом теряет смысл.
Понимание спроса
Обычная критика хедж-фондов звучит так: «Доходность Citadel 9,3% при росте S&P 500 примерно на 17% в этом году». Для большинства хедж-фондов это действительно справедливо, ведь медианный хедж-фонд — это дорогой бета-продукт.
Однако это в корне неверное представление о том, что предлагают элитные хедж-фонды вроде MLP, Citadel, P72. Эти фонды не ставят целью обогнать S&P 500. Это не их задача. Сравнивать фонд с нулевой корреляцией к акциям с 100% акционерным бенчмарком — всё равно что критиковать страховой полис за отсутствие инвестиционной доходности.
Управляя пенсионным фондом на $100 млрд, у вас уже $60 млрд в акциях. Вам не не хватает акций — вы буквально утопаете в них. Вам нужно что-то, что растет, когда акции падают (или хотя бы не падает вместе с ними). Вам нужна диверсификация. На самом деле вам нужно то, что растет всегда и приносит доход выше, чем наличные.
Это звучит очень привлекательно и, очевидно, дорого. И это действительно так! Настоящая диверсификация крайне дорога, потому что она крайне редка!
Понимание конкуренции
Долгосрочный коэффициент Sharpe для S&P 500 составляет примерно 0,35–0,50. Это значит, что на каждый 1% волатильности вы получаете 0,35–0,50% ожидаемой сверхдоходности. Лучшие хедж-фонды мира обеспечивают коэффициенты Sharpe в диапазоне 1,5–2,5 и выше.
Речь идет о поддержании коэффициента Sharpe около 2 на протяжении десятилетий; вы получаете некоррелированные потоки доходности, свободные от «дешевых» факторов, с существенно меньшей волатильностью. Просадки у таких компаний неглубокие, а восстановление быстрое.
Хедж-фонды — это не более дорогая версия того же продукта. Это совершенно другая категория. Элитные хедж-фонды предлагают две премии, недоступные для ETF и рыночных продуктов:
- Факторная нейтральность
- Высокие коэффициенты Sharpe
Факторная нейтральность
Чтобы понять, почему факторная нейтральность стоит так дорого, нужна одна формула:
r = alpha + beta * factor_returns + epsilon
r = доходность портфеля
alpha = доходность за счет навыков (интерцепт)
beta = экспозиция к системным факторам
factor_returns = доходность этих факторов
epsilon = идосинкразийный шум
Термин beta отражает ту часть доходности, которую можно реконструировать с помощью публичных факторных портфелей. Если это можно повторить, платить нужно только за репликацию. Репликация дешева: 3–9 б.п. за рыночный бета, 15–30 б.п. за стилевые факторы.
Термин alpha — это то, что остается после учета всего, что можно повторить. По определению, его нельзя синтезировать из факторных экспозиций. Эта невозможность репликации — основа премии.
Вот что упускают большинство критиков: бета дешева, потому что факторная доходность — общественное благо с неограниченной емкостью. Если рынок растет на 10%, все с рыночной экспозицией получают те же 10%. Нет ограничений. Доходность S&P 500 не уменьшается из-за роста числа держателей. Можно вложить $10 трлн в рыночный бета, и все получат одинаковый процент доходности.
Альфа дорога, потому что это игра с нулевой суммой и жесткими ограничениями по объему. Каждый доллар альфы, полученный одним, теряет другой. Неэффективности, генерирующие альфу, существуют в ограниченном количестве и сокращаются по мере роста капитала. Стратегия, дающая Sharpe 2,0 на $100 млн, может дать Sharpe 0,8 на $10 млрд, потому что сам объем торговли меняет цены и устраняет возможности арбитража. Поэтому элитные фонды закрыты для новых средств. Это не эксклюзивность ради статуса, а защита дефицита, оправдывающего комиссию.
Факторная нейтральность (beta ≈ 0 по всем системным экспозициям) — единственная конфигурация, при которой поток доходности реально невозможно повторить. В этом и заключается оправдание премии. Не в самой доходности, а в невозможности получить ее иным способом.
Высокие коэффициенты Sharpe
Эффект сложных процентов при очень высоких коэффициентах Sharpe проявляется со временем. Два портфеля с одинаковой ожидаемой доходностью 7%, но разной волатильностью (16% против 10%) дадут совершенно разные результаты за 20 лет. Портфель с меньшей волатильностью имеет вдвое меньшую вероятность потерь и лучшую защиту от снижения.
Если вы институциональный фонд с обязательствами по расходам, такая надежность стоит дополнительных затрат.
Большинство понимают волатильность как «насколько неровно идет процесс». Это верно, но не полностью. Волатильность математически снижает сложную доходность даже при одинаковых ожидаемых доходностях.
Вот формула, определяющая долгосрочное создание капитала:
Геометрическая доходность ≈ Арифметическая доходность – (Волатильность²/2)
Это называется волатильностным торможением, и арифметическая реальность такова: портфель с высокой волатильностью сильно уступает портфелю с низкой волатильностью в долгосрочной перспективе.
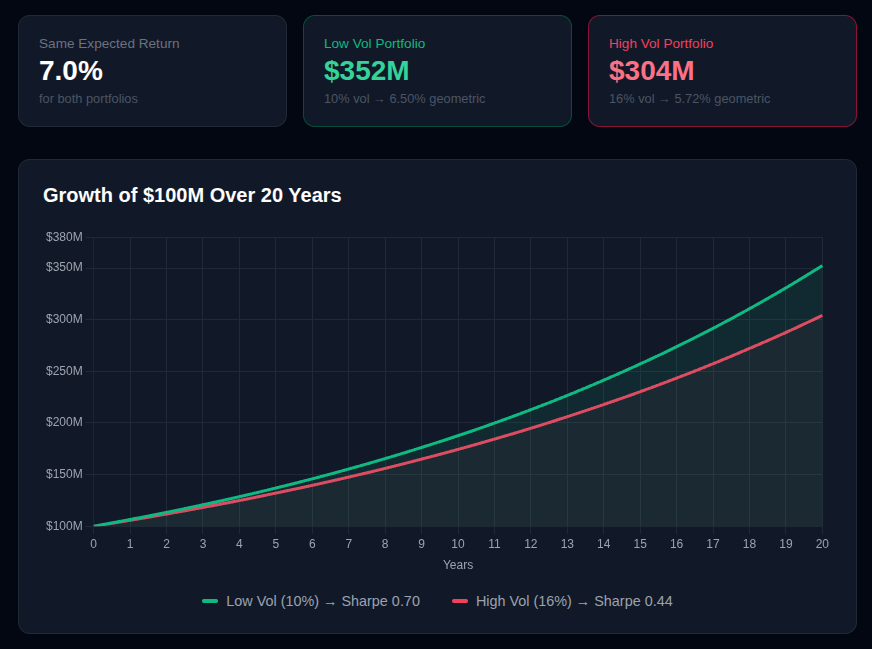
Портфель с низкой волатильностью приносит на $48 млн больше, что на 16% увеличивает итоговое состояние, несмотря на одинаковую «ожидаемую доходность». Это не вопрос предпочтения риска, а математический факт: волатильность разрушает капитал со временем.
Думайте как аллокатор
Хотите понять, почему аллокаторы готовы платить примерно в 100 раз больше за факторно-нейтральные фонды? Все дело в портфельной математике.
Условный институциональный портфель: 60% акций, 40% облигаций. Это примерно 5% ожидаемой доходности, 10% волатильности и коэффициент Sharpe 0,5. Достойно, но не выдающеся. И высокая экспозиция к рискам акций.
Добавьте 20% в факторно-нейтральные хедж-фонды с ожидаемой доходностью 10%, волатильностью 5% и коэффициентом Sharpe 2,0, без корреляции с акциями и облигациями. Новое распределение: 48% акций, 32% облигаций, 20% хедж-фондов.
Вы получаете более высокую ожидаемую доходность (6%) и меньшую волатильность (8%). Коэффициент Sharpe увеличивается на 50% (~0,75).
Это один некоррелированный хедж-фонд. Если найдете два? Три? Тогда видно, насколько ценны несколько эффективных хедж-фондов, не коррелирующих друг с другом.
Поэтому аллокаторы борются за доступ к элитным фондам. Не потому, что они не заметили, что VTI дешевле, а потому, что понимают основы портфельной арифметики. Сравнение не в комиссиях, а в том, что эти комиссии дают с точки зрения эффективности портфеля.
Как находить инвестиции как аллокатор
Допустим, вы хотите найти и оценить фонды, максимально близкие к элитным хедж-фондам. У вас нет доступа к Citadel, Millennium, Point72, но есть много времени. Можете ли вы перебрать множество фондов и определить, достойны ли они статуса «элитного» хедж-фонда?
Вот на что стоит обратить внимание:
Вычисляйте отчеты по факторной экспозиции во времени. Не только текущие значения, но и динамику за годы. По-настоящему факторно-нейтральный фонд показывает почти нулевую загрузку по рыночным, секторным и стилевым факторам стабильно. Если видите, что бета к рынку 0,3 «приходит и уходит», это тайминг факторов — может быть полезен, но это не тот продукт, за который стоит платить.
Проверяйте факторную нейтральность в стрессовых периодах. Любой фонд может показать низкую корреляцию в спокойные времена. Тест — кризисные периоды: 2008, 2020, март 2020, 2022. Если их просадки совпадали с рыночными, это не факторная нейтральность. Они тайно загружают бета.
Ищите высокие коэффициенты Sharpe на длительных периодах. Можно получить очень высокий Sharpe за короткое время по чистой случайности, но длительный период с высоким Sharpe значительно снижает вероятность случайности. Sharpe — это масштабированный t-стат доходности.
Примите, что это невозможно повторить с помощью факторных ETF. Факторные ETF дают экспозицию к value, momentum, size и т.д. за 15–50 б.п. Это не тот продукт. Факторные ETF коррелируют с факторами. Факторно-нейтральные фонды — нет. Вся суть в структуре корреляций. Нужно искать активно управляемые фонды или продукты генерации альфы.
Распознавание дефицита
Если вы сделаете все вышеописанное, скорее всего, придете к выводу, что общее число продуктов, соответствующих всем этим критериям, — 0! Если найдете — не рассказывайте мне, не публикуйте — просто инвестируйте и радуйтесь находке!
Серьезно: возможно, такие инвестиции можно найти, но они почти наверняка не смогут принять объем, необходимый институциональным аллокаторам. Возможность вложить менее $100 млн неинтересна суверенному фонду с капиталом около триллиона долларов.
Тогда вы, вероятно, правильно заключите, что только несколько компаний показали коэффициент Sharpe выше 2, на объеме более $50 млрд, за периоды, охватывающие несколько рыночных циклов. Это крайне сложно. Сочетание факторной нейтральности, масштаба и долгосрочности — редкость. Этот дефицит оправдывает премию для тех, кто может получить к ней доступ.
Заключение
Премия в 50–100 раз за элитные факторно-нейтральные хедж-фонды оправдана портфельной математикой, которую игнорируют критики. Аллокаторы не наивны. Реальный скандал — слишком много фондов берут элитную комиссию, предоставляя дорогой бета, который можно купить за 15 б.п.
(P.S: Когда фонды публикуют доходность NET OF COSTS, они уже включают дополнительные комиссии, так что ничего дополнительно вычитать не нужно).
Отказ от ответственности:
- Статья перепечатана с [systematicls]. Все авторские права принадлежат оригинальному автору [systematicls]. В случае возражений против перепечатки свяжитесь с командой Gate Learn, и они быстро решат вопрос.
- Отказ от ответственности: Мнения и взгляды, выраженные в статье, принадлежат только автору и не являются инвестиционной рекомендацией.
- Переводы статьи на другие языки выполняет команда Gate Learn. Если не указано иное, копирование, распространение или плагиат переведенных материалов запрещены.
Похожие статьи

Что такое Tronscan и как вы можете использовать его в 2025 году?
Что такое индикатор кумулятивного объема дельты (CVD)? (2025)

Что такое Нейро? Все, что вам нужно знать о NEIROETH в 2025 году

Что такое Solscan и как его использовать? (Обновление 2025 года)

15 криптовалютных проектов уровня 1 (L1), на которые стоит обратить внимание в 2024 году


